这是一篇 text to 3D 方向的突破性的文章，效果确实非常棒，据说一作的朋友圈中也说“他们将这个领域从20分提升到了70分的水平”，预测之后会有许多基于该方法的优秀文章与产品出现，毕竟之前 SDS follow 的文章也有很大一批。本阅读笔记就简要去记录一下这篇论文的主要方法和思想。

Variational Score Distillation (VSD) 是将之前提出的 Score Distillation Sampling (SDS)方法进行了泛化，换言之文章证明了 SDS 是 VSD 的一个特殊情况。目前所有 2D to 3D 做生成的基本都是基于 SDS 方法（DreamFusion），也有基于 SJC 的工作，但二者方法大体上基本一致，取得了一定的效果。

背景

论文首先简要回顾一下 Diffusion 和 SDS 方法。

Diffusion Models

对于前向过程 ${q_t}_{t \in [0, 1]}$

会向数据点 $x_0$ 逐渐添加噪声 $x_0 \sim q_0(x_0)$ ，反向过程 ${p_t}_{t \in [0, 1]}$ 生成数据。

前向满足 $q_t(x_t \vert x_0) = \mathcal N(\alpha_t x_0, \sigma_t^2 I)$ 且反向满足 $q_t(x_t) = \int q_t(x_t \vert x_0) q_0(x_0) \mathrm d x_0$ （相关推导可以看原版Diffusion Model 的内容，网上很多）。 这里的 $\alpha_t$ 和 $\sigma_t$ 为超参，满足 $\alpha_0 \approx 1, \sigma_0 \approx 0, \alpha_1 \approx 0, \sigma_1 \approx 1$ （即 $\lim_{t \to 1} q_t(x_t \vert x_0) \approx \mathcal N(0, I)$ ）

为了学习这个反向的过程，也就是生成的过程，这里需要训练一个降噪的网络 $\epsilon_\phi (x_t, t)$ ，用如下经典 loss 去训练：

$\omega(t)$ 是关于 $t$ 的一个权重函数（这个 MSE loss 意义是让网络预测的噪声 $\epsilon_\phi(\alpha_t x_0 + \sigma_t \epsilon)$ 尽量贴近真实噪声 $\epsilon$ ）。这样保证了在 $p_t \approx q_t$ 情况下满足可以采样出 $p_0 \approx q_0$ 。这里可以用 SDE 那篇文章中的 score function 表示 $\nabla_{x_t} \log q_t(x_t) \approx \nabla_{x_t} \log p_t(x_t) \approx - \epsilon_{\phi} (x_t, t) / \sigma_t$ 。

对于常见的 text-to-image 生成过程，用的是 $\epsilon_\phi(x_t, t, y)$ 其中 $y$ 为 text prompt，classifier-free guidance（CFG）是常用的方法，用于平衡多样性和质量。用 $\hat \epsilon_\phi(x_t, t, y) := (1+s)\epsilon_\phi(x_t, t, y) - s \epsilon_\phi(x_t, t, \emptyset)$ 来表示，其中 $s$ 为 guidance scale。

Text-to-3D 生成 score distillation sampling (SDS)

SDS方法顾名思义就是用来蒸馏预训练好的扩散模型，目前已经成了 2D-to-3D 路线中唯一的一个方法。即如果有预训练好的 2D Diffusion 模型 $p_t(x_t \vert y)$ 与网络 $\epsilon_{\mathrm{pretrain}} (x_t, t, y)$ ，那么 SDS 会优化在一个参数 $\theta \in \Theta$ 下的 3D 表达。

引入一些符号：相机参数 $c$ （内参+外参）、分布 $p(c)$ 以及可微渲染函数 $g(\cdot, c): \Theta \to \mathbb R^d$ 。$q_t^\theta(x_t \vert c)$ 为渲染图 $g(\theta, c)$ 在时刻 $t$ 前向扩散过程中的分布（这里分布指的是 2D Diffusion）。

那么对于 SDS 他们需要优化的是参数 $\theta$ ，即最小化 loss：

即让可微渲染图在第 $t$ 步扩散与预训练模型的分布近似，从而让最后整体在 $t \to 0$ 的分布进行近似，用这里 KL 散度保证这个事情。

我们要优化这个得分函数，只需要求得这个梯度，可以近似为 \(\begin{equation} \nabla_\theta \mathcal L_{\mathrm{SDS}}(\theta) \approx \mathbb E_{t, \epsilon, c} [\omega(t)(\underbrace{\epsilon_{\mathrm{pretrain}}(x_t, t, y) - \epsilon}_{\mathrm{Noise ~Residual}}) \underbrace{\frac{\partial g(\theta, c)}{\partial \theta}}_{\mathrm{Generator~Jacobian}}] \end{equation}\) 这就是基于 SDS 的核心逻辑 $\theta_{i+1} = \mathrm{opt.step}(\theta_i, \nabla_\theta \mathcal L(x_i))$ ，不断去优化下一个对应获得参数。相关推导以及理论可以参考 DreamFusion 及其引用。

3D 表示

这里用经典的 NeRF（Neural Radiance Fields）和 DMTet（Deep Marching Tetrahedra）两种主流方法作为 3D 表示。

• NeRF 用 MLP 表示3D，利用 $(x, y, z)$ 坐标输入得出 $(r,g,b,\sigma)$ 即颜色与密度表示。这里 $\theta$ 为 MLP 的参数，那么给出相机位姿 $c$ ，就有渲染可微渲染函数 $g(\theta, c)$ ，意义为从每个像素发射射线，计算沿着每条射线采样点的颜色的加权和，合成每个像素的颜色。NeRF在优化方面非常灵活，并能够表示极其复杂的场景。

• DMTet 这种方法是需要拉出三角网格，用网格点的颜色表示纹理。这里的 $\theta$ 为三角网格坐标和纹理的参数，那么有可微渲染函数 $g(\theta, c)$ ，意义为从像素发射射线并计算射线与网格表面的交点来获得每个像素的颜色。这个方法消耗显存小，并且渲染非常快，所以可以支持高像素，但是对于复杂场景支持一般。

Variational Score Distillation（VSD）

这篇文章提出的核心就是 VSD ，通过在 3D场景的分布中采样，用3D参数 particles 去表示 3D 分布，基于 Wasserstein 梯度流推导出一种基于梯度的 particles 更新规则。

从3D场景中采样进行变分推断

和前面一致，若有 text prompt $y$ ，那么就存在一个对于所有 3D 表示的随机概率分布，在一个 3D 参数 $\theta$ 表示下，这个分布我们可以记成一个概率密度函数 $\mu(\theta \vert y)$ 。并且记 $q_0^\mu (x_0 \vert c, y)$ 为渲染图 $x_0 := g(\theta, c)$ 的隐式分布（我的理解是这个为基于网络参数对渲染图的分布表达），那么有 $q_0^\mu(x_0 \vert y) := \int q_0^\mu (x_0 \vert c, y) p(c) \mathrm{d} c$ 为这个的边缘分布（对于原来联合分布相对于相机分布 $p(c)$ 的部分）。并且我们这里记 $p_0(x_0 \vert y)$ 为 $t = 0$ 时预训练的 2D Diffusion 的边缘分布。

那么需要获得高质量的 3D 表示的话，作者在这里提出了用 KL Loss 拟合这个边缘分布的方法：

这是一个经典的变分推断问题，用变分分布 $q_0^\mu (x_0 \vert y)$ 去近似目标分布 $p_0(x_0 \vert y)$ ，前者的边缘分布意义可以理解为没有相机渲染视角指导下的图片分布，其应该对应上 2D Diffusion 从 web scale 图片下获取的分布。

直接最优化这个函数是比较复杂的，因为 $p_0$ 是相当复杂的一个分布，并且在高维空间中这个分布的高密度区域是很稀疏的。有一种解释是如果这个分布是支撑在高维空间中的低维流形时，他们重叠部分的测度为 $0$ 的概率几乎是 $1$ ，这样直接去近似的 Loss 是很难下降的。

但仍可以借鉴扩散模型的思路去转化为优化每一个 $t$ 的扩散分布，这个之前有许多成功的先例，形如 SDS ，这里就使用变分分数蒸馏（VSD）方法去优化这个 loss：

这里大部分定义和前面 SDS 可以类比的，其中分布定义有 $q_t^\mu(x_t \vert c, y) := \int q_0^\mu (x_0 \vert c, y) p_{t0}(x_t \vert x_0) \mathrm d x_0$ ，类似地 $q_t^\mu(x_t, y) := \int q_0^\mu (x_0 \vert y) p_{t0}(x_t \vert x_0) \mathrm d x_0$ 为前者的边缘分布，并且 $p_t(x_t \vert y) = \int p_0(x_0 \vert y) p_{t0} (x_t \vert x_0) \mathrm d x_0$ 为时间 $t$ 对应的加噪分布，根据Diffusion Model 的推导有 $p_{t0} (x_t \vert x_0) = \mathcal N(x_t \vert \alpha_t x_0, \sigma_t^2 I)$ ，这里 $\omega(t)$ 与前面的定义类似为时间权重函数。等式成立的条件是因为联合分布和边缘分布在 KL 散度下的一致性。

这里就可以发现该方法与 SDS 的区别了，SDS是为了3D表示的参数 $\theta$ 也就是单个数据点，但 VSD 是为了得出整体 3D的概率分布空间 $\mu$ ，从整个空间中我们再采样出数据点 $\theta$ 。

而且作者在附录中证明了优化这个额外 KL loss 就可以达到最初近似分布的目的，即对于任意 $t>0$ 都有

VSD 的更新方法

为了解决

最简单的方法是训练另一个以 $\mu$ 为参数的生成模型，但这会带来许多计算上的消耗。这里介绍了 particle-based 的变分推断方法，即使用 $n=4$ 个（平衡效果和计算消耗）3D 参数 ${\theta}_{i = 1}^n$ 作为 particles 并且遵循一个更新法则。直观地说，用这 $n$ 个 particles 来代表当前的分布 $\mu$ ，并且 $\theta^{(i)}$ 会从优化后的分布 $\mu^*$ 中进行采样（如果收敛的话）。

这样的优化过程可以被写成模拟一个关于 $\theta$ 的 ODE 的过程，下面进行描述：

• 对于 VSD 的 Wasserstein 梯度流：

  Wasserstein梯度流：基于Wasserstein距离的梯度信息，定义了一个概率分布随时间演化的微分方程。在Wasserstein梯度流中，考虑一个初始概率分布 $P_0$ 和目标概率分布$P_T$ ，目标是找到一个时间依赖的概率分布 $P(t)$ ，其中 $t$ 在 $[0, T]$ 范围内变化，使得 $P(t)$ 在每个时间点 $t$ 的 Wasserstein 距离与目标分布 $P_T$ 最小化。

  剩余相关证明和推导可以见原文附录，下面仅作定理叙述。

  从初始分布 $\mu_0$ 开始，对于任意时刻 $\tau \ge 0$，记在分布空间最优化 $\mu^{\star}$ 过程的 Wasserstein 梯度流为 ${\mu_\tau}_{\tau \ge 0}$

  其中 $\mu_\infty = \mu^{\star}$ ，那么我们可以从 $\mu_\tau$ 中采样 $\theta_\tau$ ，首先采样 $\theta_0 \sim \mu_0 (\theta_0 \vert y)$ 然后之后的用如下 ODE 进行模拟：

  \[\frac{\mathrm d \theta_\tau}{\mathrm d \tau} = - \mathbb E_{t, \epsilon, c} [\omega(t)(\underbrace{-\sigma_t \nabla_{x_t} \log p_t(x_t \vert y)}_{\mathrm{score~of~noisy~real~images}} - \underbrace{(-\sigma_t \nabla_{x_t} \log q_t^{\mu_\tau}(x_t \vert c, y) ))}_{\mathrm{score~of~noisy~rendered~images}} \frac{\partial g(\theta_\tau, c)}{\partial \theta_\tau}]\]

只需要求出足够大的 $\tau$ ，就能近似到希望求出的分布 $\mu^{\star}$ 。

右式类似于 SDS 的梯度求法，其中对于 score of noisy real images $-\sigma_t \nabla_{x_t} \log p_t(x_t \vert y)$ 可以直接用预训练好的 2D Diffusion 降噪网络 $\epsilon_{\mathrm{pretrain}} (x_t, t, y)$ 进行近似，对于后者 $- \sigma_t \nabla_{x_t} \log q_t^{\mu_\tau} (x_t \vert c, y)$ 我们这里采用另外一个降噪网络 $\epsilon_\phi (x_t, t, c, y)$ 进行近似，这个我们用 ${\theta^{(i)}}_{i = 1}^n$ 渲染好的图片以及标准的Diff Loss 进行训练： \(\min_{\phi} \sum_{i = 1}^{n} \mathbb E_{t \sim \mathcal U(0, 1), \epsilon \sim \mathcal N(0, I), c \sim p(c)} [ \vert\vert \epsilon_\phi(\alpha_t g(\theta^{(i)}, c) + \sigma_t \epsilon, t, c, y) - \epsilon\vert\vert_2^2]\) 即用这个 MSE Loss 去拟合这个标准噪声。

这篇文章用了一个 U-Net 或者对于原来预训练模型 $\epsilon_{\mathrm{pretrain}} (x_t, t, y)$ 的 LoRA 去表示这个参数 $\epsilon_\phi$ ，并且添加了相机的位姿 $c$ 作为 condition embedding 到网络中。作者根据实验说 LoRA 在 few-shot 下的保真度非常好。

注意到对于每个 ODE 的时刻 $\tau$ ，需要去确认 $\epsilon_\phi$ 符合当前的 3D分布 $q_t^{\mu_\tau}$ ，这样需要轮流优化 $\epsilon_\phi$ 和 $\theta^{(i)}$ 。对于 particle 我们用 $\theta^{(i)} \leftarrow \theta^{(i)} - \eta \nabla_\theta \mathcal L_{\mathrm{VSD}} (\theta^{(i)})$ 进行优化（其中 $\eta > 0$ 为 learning rate），由之前的式子，这个梯度可以被表示为 \(\nabla_{\theta} \mathcal L_{\mathrm{VSD}} (\theta) \triangleq \mathbb E_{t, \epsilon, c} [\omega(t) (\epsilon_{\mathrm{pretrain}}(x_t, t, y) - \epsilon_\phi (x_t, t, c, y) \frac{\partial g(\theta, c)}{\partial \theta}]\) 在这里有 $x_t = \alpha_t g(\theta, c) + \sigma_t \epsilon$ 即渲染图在时刻 $t$ 加噪后的情况。

伪代码如下：

网络结构

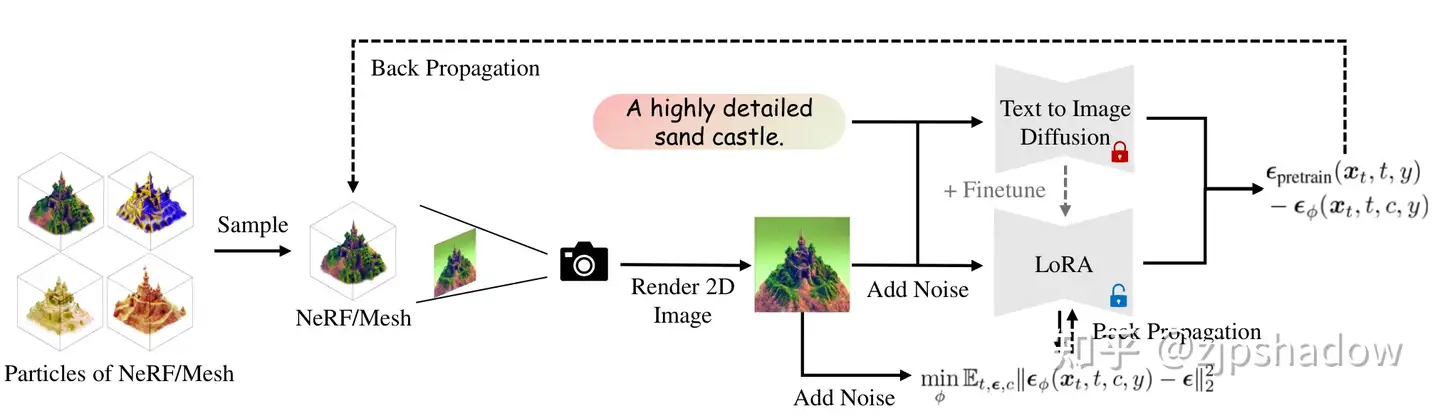
整体网络结构与 SDS 方法是类似的，结合上面的伪代码即可看懂。

• 首先随机从当前分布中采样网络的3D参数 $\theta$ ，以及相机位姿 $c$
• 然后利用可微渲染方法，渲染出对应的 2D 图片 $x_0 = g(\theta, c)$
• 而后更新3D表达的参数 $\theta$ 为 $\theta - \eta_1 E_{t, \epsilon, c} [\omega(t) (\epsilon_{\mathrm{pretrain}}(x_t, t, y) - \epsilon_\phi (x_t, t, c, y) \frac{\partial g(\theta, c)}{\partial \theta}$
• 最后更新 LoRA 中蕴含的潜在 3D 分布 $\phi$ 为 $\phi - \eta_2 \nabla_\phi \mathbb E_{t, \epsilon} \vert\vert\epsilon_\phi(x_t, t, c, y) - \epsilon\vert\vert_2^2$ ，即更加贴近原本 $q_t^{\mu_\tau}$ 的分布，如此往复直至收敛。